Last week, I calculated my own version of various advanced statistics, such as Rebound Rate, Assist Rate, and Usage Rate.  The difference between my versions and the ones you normally see are that mine were based on actual play-by-play data, rather than estimates.  Although my method isn’t perfect (partly because the play-by-play isn’t always reliable), I figured it was more accurate to base our stats on stuff that has actually happened as opposed to estimates of what happened.

Under that assumption, the question is how accurate are the numbers we’ve grown to know and love?  Although they’re not too difficult to calculate, the play-by-play figures aren’t always available, so we need to know if we can count on the data that is most common.  How far off are these estimations?  Are there certain types of players for which these stats are usually inaccurate?

To recap, these are the stats in question:

• Rebound Rate
• Offensive Rebound Rate
• Defensive Rebound Rate
• Assist Rate
• Steal Rate
• Block Rate
• Usage Rate

Let’s start with a simple test.  How well do the estimated numbers correlate with the play-by-play numbers?  Below is a table that includes the R^2 (explanation) and standard error of each linear regression, as well as the average difference between the two types:

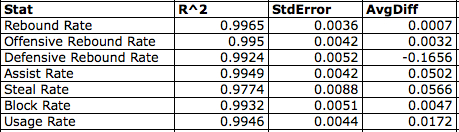
Thankfully, we see that all of the estimations appear to be pretty darn accurate.  The R^2’s are all extremely high, and the standard errors are low.  Of the seven stats I’m examining, Steal Rate appears to be the most inaccurate.  It fares the worst in each of the three table columns.  Overall Rebound Rate appears to be the most accurate.  From this table, we are given no reason to doubt the validity of the box score estimations.

Although they may be accurate as a whole, perhaps these numbers are inaccurate just for certain players.  Specifically, I was wondering if players that rate either really high or really low in a certain statistic are generally rated accurately by the box score estimation.  To try to answer that question, I ran another regression.  This time, the box score estimation was the independent variable, and the difference between the box score and play-by-play was the dependent variable.  The results are in the table below:

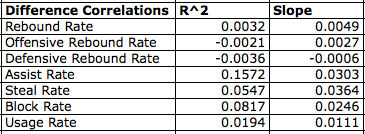
There are some things to look out for.  Although the adjusted R^2’s are all quite low, even negative sometimes, the slopes are all positive.  This would indicate that as a given player gets better in a certain statistic, the box score data is more likely to overrate him in that category.  The biggest problems occur with Assist Rate, which has a moderately sized R^2 value.

If that table doesn’t seem intuitive, I’ve also decided to present the results graphically.  In each chart below, the x-axis is the box score estimate’s value, and the y-axis is the difference between the estimate and the play-by-play calculation.

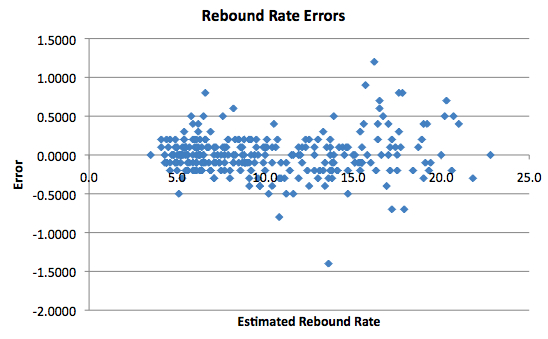
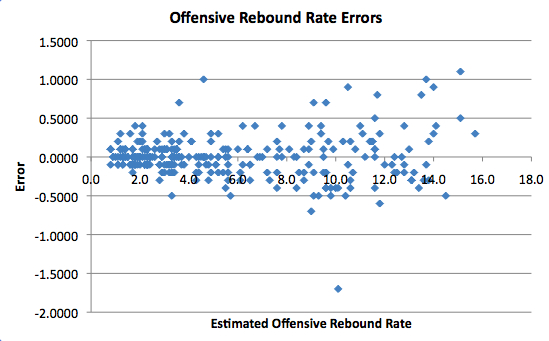
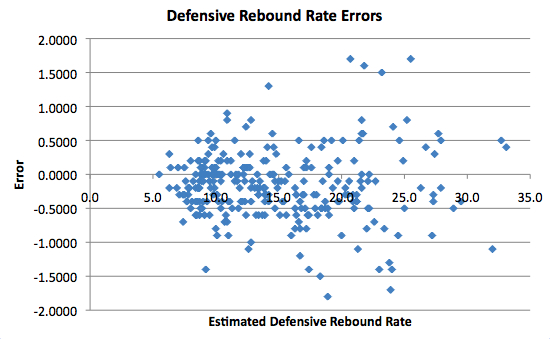
All three Rebound Rates look pretty accurate, although they become more unpredictable as the numbers get high, especially with respect to Defensive Rebound Rate.  When the Rate is around 10, the errors are pretty closely scattered around 0.   However, when you get to 17.5 or 20, the errors become larger.

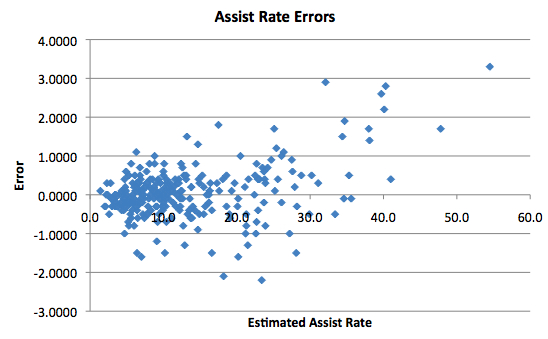
As I mentioned before, Assist Rate seems to have some major issues.  For low Assist Rates, the differences are pretty small.  However, when you get to the top assist men, the differences can be quite large.  For example, Chris Paul’s Assist Rate for last season, according to the box score data, was 54.5.  However, the play-by-play data has it at 51.2.  For someone like him, where the number is astronomically high no matter which method you choose, the difference might seem trivial.  But it does appear that top assist men are overrated the most by Assist Rate.

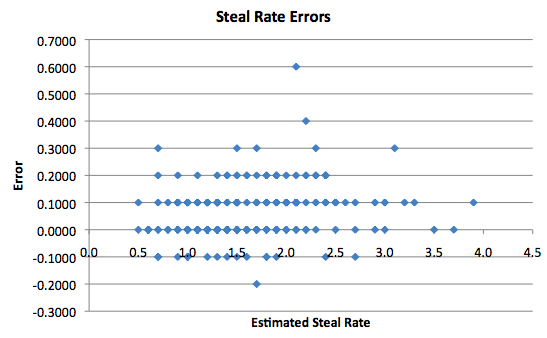
There’s not much to gather from the Steal Rate chart, although it becomes clear that my play-by-play computations are generally lower than the box score estimates.

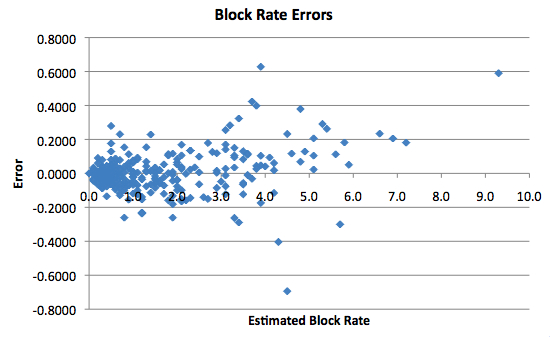
Like Rebound Rate, Block Rate becomes particularly difficult to estimate when the numbers get high.  As a percentage of the Block Rate, though, the difference is actually pretty consistent.

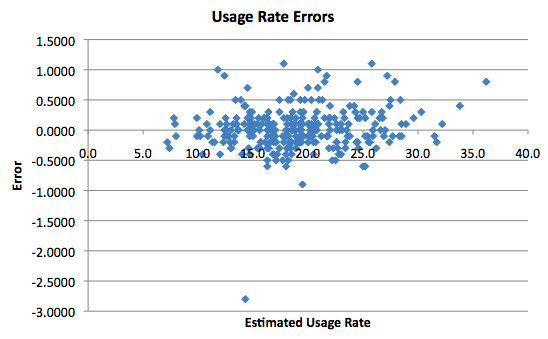
Finally, we have Usage Rate.  There aren’t any major issues except for one outlier at the bottom, which is the result of complications due to the weirdness of Luc Richard Mbah a Moute’s name (seriously).

In conclusion, my research has shown me that, despite some minor issues, the box score estimations of things such as available rebounds are actually pretty close.  They aren’t always perfect, and they can be particularly unreliable when the numbers get large, but overall they do a good job.  Hopefully this work will provoke discussion on how we can continue to perfect those stats.